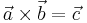Right-hand rule

In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century.[1][2]

When choosing three vectors that must be at right angles to each other, there are two distinct solutions, so when expressing this idea in mathematics, one must remove the ambiguity of which solution is meant.

There are variations on the mnemonic depending on context, but all variations are related to the one idea of choosing a convention.

Contents

Direction associated with an ordered pair of directions

One form of the right-hand rule is used in situations in which an ordered operation must be performed on two vectors a and b that has a result which is a vector c perpendicular to both a and b. The most common example is the vector cross product. The right-hand rule imposes the following procedure for choosing one of the two directions.

\vec{a} \times \vec{b} = \vec{c}

Other (equivalent) finger assignments are possible. For example, the first (index) finger can represent a, the first vector in the product; the second (middle) finger, b, the second vector; and the thumb, c, the product.[3]

Direction associated with a rotation

A different form of the right-hand rule, sometimes called the right-hand grip rule or the corkscrew-rule, is used in situations where a vector must be assigned to the rotation of a body, a magnetic field or a fluid. Alternatively, when a rotation is specified by a vector, and it is necessary to understand the way in which the rotation occurs, the right-hand grip rule is applicable.

This version of the rule is used in two complementary applications of Ampère's circuital law:

  1. An electric current passes through a solenoid, resulting in a magnetic field. When you wrap your right hand around the solenoid with your fingers in the direction of the conventional current, your thumb points in the direction of the magnetic north pole.
  2. An electric current passes through a straight wire. Here, the thumb points in the direction of the conventional current (from positive to negative), and the fingers point in the direction of the magnetic lines of flux.

The principle is also used to determine the direction of the torque vector. If you grip the imaginary axis of rotation of the rotational force so that your fingers point in the direction of the force, then the extended thumb points in the direction of the torque vector.

The right-hand grip rule is a convention derived from the right-hand rule convention for vectors. When applying the rule to current in a straight wire for example, the direction of the magnetic field (counterclockwise instead of clockwise when viewed from the tip of the thumb) is a result of this convention and not an underlying physical phenomenon.

Applications

The first form of the rule is used to determine the direction of the cross product of two vectors. This leads to widespread use in physics, wherever the cross product occurs. A list of physical quantities whose directions are related by the right-hand rule is given below. (Some of these are related only indirectly to cross products, and use the second form.)

Fleming's left-hand rule is a rule for finding the direction of the thrust on a conductor carrying a current in a magnetic field.

Left-handedness

In certain situations, it may be useful to use the opposite convention, where one of the vectors is reversed and so creates a left-handed triad instead of a right-handed triad.

An example of this situation is for left-handed materials. Normally, for an electromagnetic wave, the electric and magnetic fields, and the direction of propagation of the wave obey the right-hand rule. However, left-handed materials have special properties, notably the negative refractive index. It makes the direction of propagation point in the opposite direction.

De Graaf's translation of Fleming's left-hand rule - which uses thrust, field and current - and the right-hand rule, is the FBI rule. The FBI rule changes thrust into F (Lorentz force), B (direction of the magnetic field) and I (current). The FBI rule is easily remembered by US citizens because of the commonly known abbreviation for the Federal Bureau of Investigation.

Symmetry

Vector Right-hand Right-hand Right-hand Left-hand Left-hand Left-Hand
a, x or I Thumb Fingers or palm First or Index Thumb Fingers or palm First or index
b, y or B First or index Thumb Fingers or palm Fingers or palm First or index Thumb
c, z or F Fingers or palm First or index Thumb First or index Thumb Fingers or palm

See also

Notes

  1. ^ Fleming, John Ambrose (1902). Magnets and Electric Currents, 2nd Edition. London: E.& F. N. Spon. pp. 173–174. http://books.google.com/books?id=ASUYAAAAYAAJ&pg=PA173. 
  2. ^ "Right and left hand rules". Tutorials, Magnet Lab U.. National High Magnetic Field Laboratory. http://www.magnet.fsu.edu/education/tutorials/java/handrules/index.html. Retrieved 2008-04-30. 
  3. ^ PHYS345 Introduction to the Right Hand Rule, George Watson, University of Delaware, 1998

External links